基于拓扑排序的排课程序

一、题目描述

某学院有n门课程，（i，j）表示课程i是课程j的先行课，及课程i必须在课程j的之前的学期开设。对任意给出的仙子那个课解s={(1,3),(2,4),(3,5),(4,6),(3,7),…},至少需要安排多少个学期？给出每个学期的课程清单。

二、程序思路

分析题目能清楚地发现此题与拓扑排序有很大的关系，拓扑排序的层数就是学期数，每个学期的课程就是每一层的点。所以只需要在拓扑排序的程序上改改就好了。

三、具体实现

int linkedDgraph1::course(int **b)//传入的为保存结果的二维数组
{   
	int number=0;//学期数 
	int n=verticeNumber;//顶点个数 
	int *indegree=new int[num1+1];//顶点的入度数组 
	for(int i=1;i<=num1;i++)//保存入度 
	indegree[i]=inDegree(i);
	stack<int> astack(10000);//声明栈 
	while(n!=0)
	{      int j=0;
		 for(int i=1;i<=num1;i++)//遍历将入度为零的点入栈 
		{    
			if(indegree[i]==0)
			{ 
			  b[number][j++]=i;//保存此点 
			  //cout<<i<<" ";
	          astack.push(i);  //入栈 
		    }
		}
		   number++;//前一学期的课程已完 
		   //cout<<number<<" ";
		   while(!astack.empty())
			{  int t=astack.top();
			   n--;
			 //  cout<<verticeNumber<<" ";
			   indegree[t]=-1;
			   astack.pop();
			   for(int i=1;i<=num1;i++)//更新各顶点的入度 
			     if(existsEdge(t,i))
			      indegree[i]--;	
			} 
	}
	return number;
}

四、结果展示

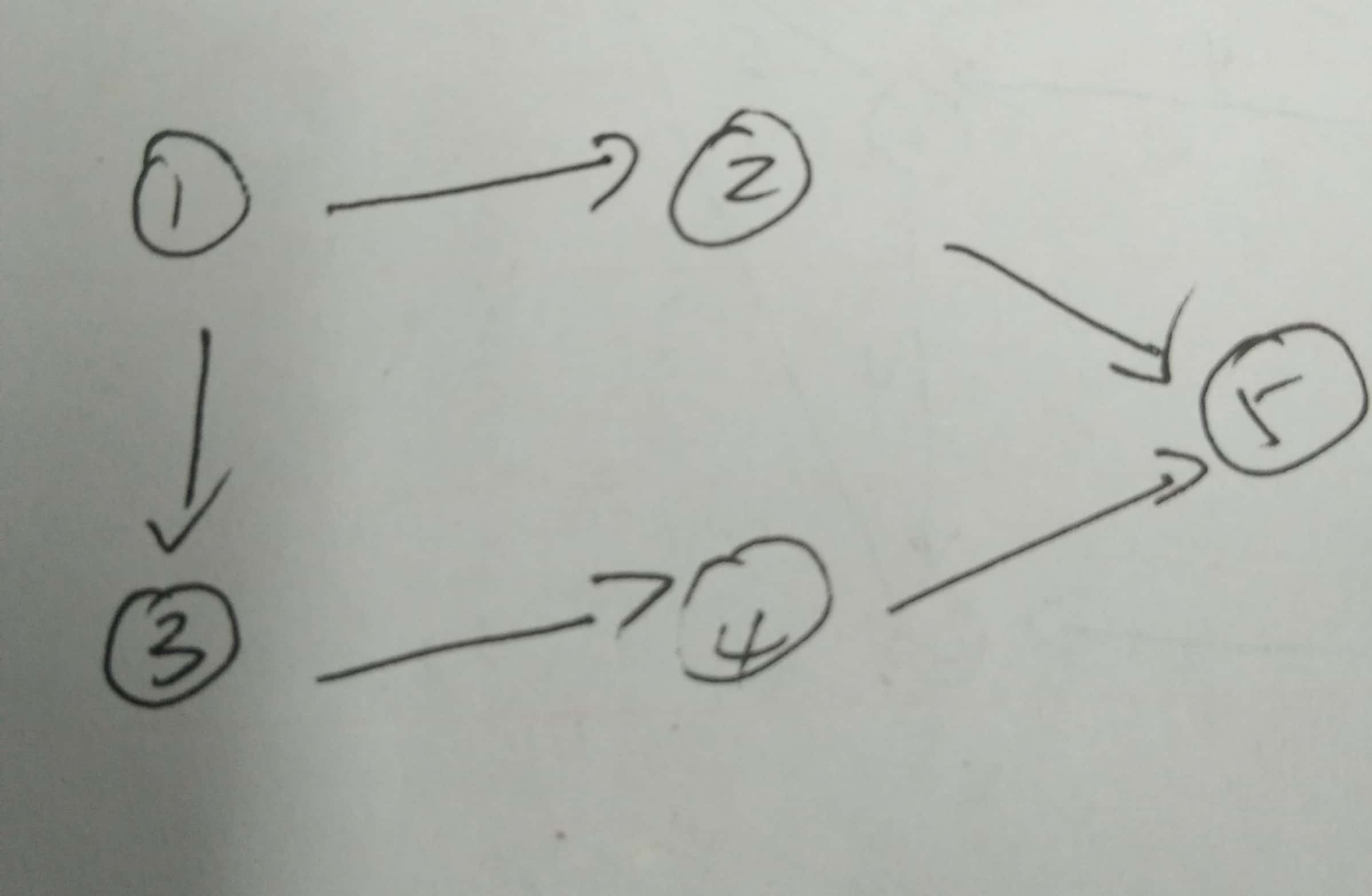
五、说明

本程序所用图的结构为邻接链表。